瞬态动力学

瞬态是系统从一个平衡状态移动到另一个平衡状态时的中间变化状态。临界阶段通常被描述为或者假定是突然和剧烈的。但在现实世界中的临界过渡通常表现出不同的时间长度, 而这主要取决于系统的大小，驱动力的频率以及系统转变的类型。如果在一个临界转换过程中外间的干扰是频繁的，那么系统也很可能表现出一系列连续的变化。更好地了解临界转变所需要的时间长度以及决定转变时间的因素对制定相应的管理措施至关重要。下图显示的是，至少在数学模型中，过渡模式在很大程度上取决于该系统对特定的驱动力的反应是快或慢, 这和系统的动态类型无关。重要的是，响应缓慢的系统总是表现出随时间而逐步由一个状态到一个状态。三大问题：我们如何知道一个区域的社会-生态系统已经跨过了转折点？它达到一个新的状态需要多长时间？新的状态是什么样子？

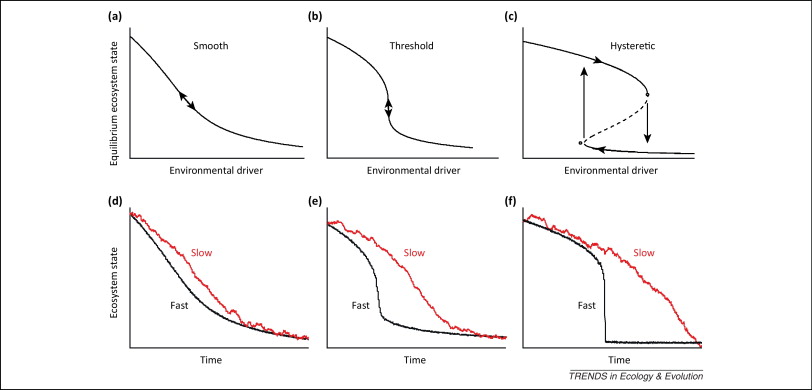
图：一个动态系统（平衡状态）对缓慢变化的条件或环境驱动的响应可以是（a）平稳过程，（b）阈值依赖过程或（c ）临界转化-折迭突变过程。图（d-f ）是应对不断升级的驱动条件下的系统响应模拟过程。在每个图上的两条曲线代表快速（黑线）和慢速（红线）响应系统。模拟结果表明，快速响应的系统表现出的轨迹，从渐进的（d）、快速（e）的、到突然的（f ）变化，取决于系统动力学改变；但慢速响应系统总是表现出随时间而逐步发生状态变化，即使越过了急剧的阈值改变（Hughes等，2013 ）。